Try GizAI for free, no login

Discover the ultimate AI content creation experience with GizAI—a robust, free AI platform that requires no sign up to get started. In today’s fast-paced digital world, users want innovative tools that empower them instantly, without long registration processes or subscription hassles. GizAI has emerged as a game-changing ecosystem designed for writers, marketers, game designers, and creative professionals. In this article, we explore every powerful feature GizAI has to offer while highlighting its free, no sign up experience, helping you unlock a whole new era of AI-driven creativity.

GizAI combines state-of-the-art artificial intelligence with real-time collaboration and cloud storage, enabling users to generate images, videos, audio, characters, stories, games, and even interactive chat narratives—all from a single text prompt and without compromising privacy. With increasing demand for free AI tools that require no sign up, GizAI stands out by blending advanced technology with user-centric simplicity.

Unleashing the Power of Free AI Without Registration

One of the most attractive aspects of GizAI is its commitment to accessibility. As many leading platforms insist on user registration and paid subscriptions, GizAI proves that powerful content creation does not have to come at a premium cost or require lengthy sign up procedures. The platform’s no sign up policy means that creativity is available directly from the browser—no barriers, just instant access.

The free plan is meticulously designed to make advanced content generation accessible, protecting user privacy by not training the AI with personal data or sharing it without consent. With a proven reputation of providing free access to essential creative tools, GizAI has built its brand around the motto: AI access is a human right. This unique approach not only reduces the friction involved in getting started with AI tools but also establishes moral credibility for the platform in the realm of digital innovation.

Comprehensive Features That Inspire Creativity

GizAI is packed with features that cater to a wide range of creative needs:

1. AI-Powered Content Generation

GizAI’s core strength lies in its multi-modal AI models that generate content across various formats. Whether you need a captivating story, an engaging video, or stunning images, the platform has dedicated generators to turn your text prompt into multimedia masterpieces. This eliminates the need to juggle between different platforms and tools, making professional-level content creation more streamlined than ever before.

Examples of supported content types include:

• Image Generation: Use advanced text-to-image generators that create detailed visuals based on your description. The underlying models maintain object consistency and style coherence—a crucial factor for brand identity and storytelling.

• Video and Audio Production: Not only can you generate images, but GizAI also supports video and audio creation, enabling dynamic multimedia storytelling. With real-time collaboration features, teams can work together to craft polished final products.

• Text and Storytelling: Enhance your narrative writing with AI assistance. Generate engaging plotlines, character details, dialogues, and even interactive story-based games that captivate your audience.

Users can experiment with various art styles, making every creation uniquely tailored to their creative vision.

2. Interactive Story-Based Games and Custom Narratives

GizAI is uniquely designed to support interactive storytelling and game creation. Content creators can build immersive narratives complete with branching storylines and character dialogs. This feature caters especially to novelists, screenwriters, and game designers who want to create interactive experiences that engage their audiences on multiple levels.

The context-aware naming tool and character generator take creative writing to new heights by offering suggestions that align with your story’s overall theme. The interactive component ensures that every piece of content—whether a game or a narrative—is consistent, engaging, and tailored to the intended audience.

3. Real-Time Collaboration and Cloud Storage

A standout feature of GizAI is its seamless integration with real-time collaboration tools and cloud storage. This functionality is essential for teams working remotely or individuals collaborating with peers across geographies. By synchronizing content across devices and enabling simultaneous edits, GizAI makes it effortless to brainstorm, refine, and perfect your creative output in real time.

Cloud storage ensures that all your creative projects are securely saved online, with robust privacy controls that guarantee user data is never used for training AI models without consent. This is particularly appealing in an age where data privacy is paramount.

4. Mind Map and Response Format Options

GizAI offers a revolutionary mind map response option in its AI chat assistant. Users can request their responses to be formatted as a mind map—a visual representation that helps break down complex ideas into easily digestible sections. This interactive feature is especially beneficial for planning large projects, outlining articles, or restructuring intricate narratives.

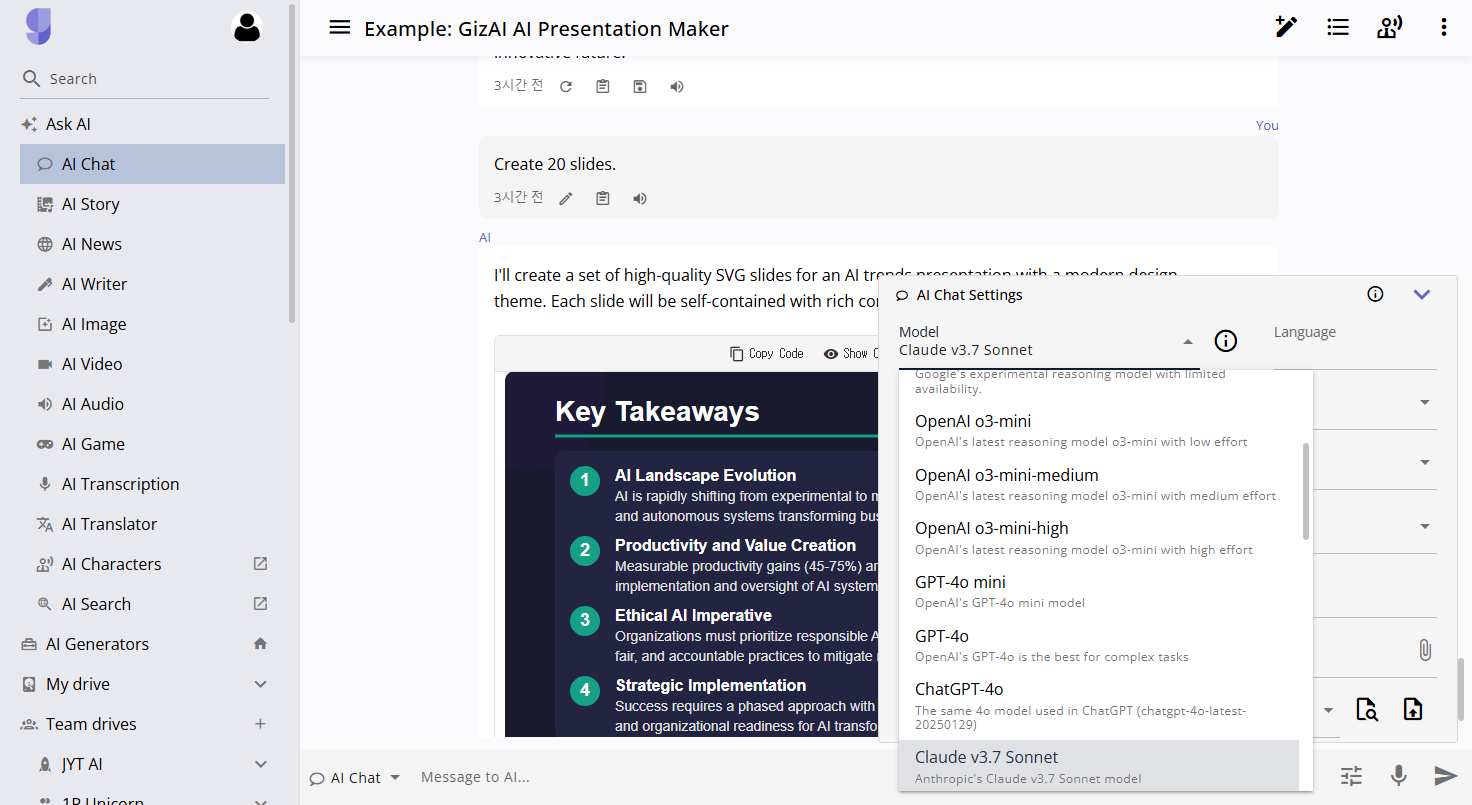
Additionally, users have the flexibility to switch between various response formats, including dynamic text, media-included answers, web app views, slides, or traditional text. This format versatility empowers creators to present their information exactly how they envision it.

5. Multi-Language Support

As GizAI continues to expand its global reach, the platform now supports multiple languages including Spanish, Portuguese, French, German, Italian, Russian, Chinese, Japanese, and Korean. This makes it an invaluable tool not just for native English speakers but for creative professionals worldwide, democratizing access to high-quality AI content generation regardless of language barriers.

6. No Sign Up, No Hassle, Just Creativity

Perhaps the most enticing feature of GizAI is its free plan which requires absolutely no sign up. Unlike other platforms that often demand personal information or payment details even for trial usage, GizAI’s no registration policy eliminates the barrier to entry. Users can immediately access all the core functionalities and experience hassle-free creativity. This approach has garnered positive feedback from communities that appreciate streamlined workflows and immediate access to sophisticated tools.

What Sets GizAI Apart in the Competitive AI Ecosystem?

In the rapidly evolving field of AI content creation, GizAI stands apart for several reasons:

Privacy and Data Security

GizAI is dedicated to protecting user privacy. The platform does not train its AI models with user-generated data without consent, ensuring that your creative ideas remain confidential. This commitment to security is a crucial trust factor in today’s digital landscape, especially when compared with other free tools that may compromise data integrity in exchange for broader training datasets. Users confidently explore their creative potential knowing their intellectual property is safeguarded.

Collaborative Environment

The built-in support for collaborative work sets GizAI apart from similar platforms that focus solely on individual creativity. In today’s interconnected world, the ability to develop content in a team setting without disruptions adds massive value. From brainstorming sessions to full-scale project creation, GizAI facilitates a seamless collaboration experience that rivals professional software suites—all while remaining free and accessible.

Multi-Modal Content Creation

While many competitors focus on one type of content generation, GizAI’s multi-modal approach allows for the creation of visuals, texts, audios, videos, and interactive games under one roof. This diversity in content generation eliminates the need for multiple subscriptions or software licenses, providing users a comprehensive toolset that suits any creative purpose. Whether you’re a digital marketer, a freelance writer, or a game developer, GizAI’s all-in-one solution caters to your specific needs.

Accessibility through Free and Unrestricted Features

It’s not just the functionality that makes GizAI impressive; it’s also the philosophy of making advanced AI tools accessible to everyone, regardless of budget. Free access without sign up means anyone—from students to professionals—can harness the power of AI for creative projects instantly. This uninterrupted access promotes a culture of innovation and experimentation, encouraging more users to explore the potential of AI in content creation. (Inline Source links)

Real-World Applications of GizAI’s Free AI Tools

To truly appreciate the versatility of GizAI, let’s take a closer look at some of the practical applications and use cases:

Digital Marketing and Branding

For digital marketing professionals and brand strategists, the ability to quickly generate high-quality content is a game-changer. GizAI’s advanced image generator, for example, can create visually appealing graphics for social media campaigns that captivate audiences and increase engagement. The platform’s automatic content creation features enable marketers to craft compelling narratives that resonate with their target audience—all without the delay of traditional creative processes.

Furthermore, the custom name generator helps brands create unique product and character names that are both memorable and aligned with their overall messaging. With consistent naming conventions throughout campaigns, brands maintain a strong identity while saving time and resources that would typically be spent brainstorming ideas. (Inline Source links)

Content Creation and Blogging

Bloggers and freelance writers can significantly benefit from GizAI’s text and story generators. The platform’s AI-driven content creation tools are built to help generate ideas, structure articles, and refine drafts quickly. Whether you’re crafting a personal blog post or a detailed long-form article, GizAI’s capability to maintain narrative consistency and generate citations correctly streamlines the writing process.

Moreover, the mind map response format is especially useful for outlining and organizing complex topics before diving into the writing process. It not only simplifies the ideation stage but also provides a visual roadmap that can boost productivity and clarity. The free, no sign up approach means that writers can experiment freely with different styles and techniques without worrying about subscription costs. (Inline Source links)

Interactive Storytelling and Game Development

GizAI’s impact is not limited to traditional content; it extends into the realm of interactive storytelling and game development. Creative professionals designing digital games can use the platform to generate storylines, character details, and even branching narratives that offer multiple outcomes based on user choices. This type of interactivity enhances user engagement and creates a deeper connection with the audience.

For independent game developers working with limited budgets, the ability to leverage advanced AI for content generation without incurring high costs is invaluable. The integration of collaborative tools also means that teams working remotely can innovate together in real time, ensuring that every element of the project—from dialogue to visual style—is perfectly synchronized. (Inline Source links)

Educational and Training Purposes

Educators and trainers are finding innovative ways to incorporate AI-generated content into their lesson plans and training modules. With multi-language support and flexible formatting options, GizAI can be used to create customized educational materials, interactive quizzes, and engaging multimedia presentations. This not only aids in the learning process but also introduces students to the practical applications of AI in modern content creation—a skill that is increasingly valuable in many career fields.

For instance, academic professionals can generate detailed tutorials on complex subjects or simulate interactive storytelling experiences that bring historical events to life. The free access without sign up ensures that educators can experiment and integrate these tools seamlessly into their classrooms, providing a modern twist to traditional teaching methods. (Inline Source links)

Creative Arts and Personal Projects

Artists and hobbyists are also reaping the benefits of GizAI’s free AI creativity tools. Whether you’re looking to create digital artwork, compose music, or even write a novel, GizAI offers a platform that nurtures creative expression. The intuitive interface and variety of creative options empower users to experiment with new styles and techniques without the limitations imposed by steep learning curves or costly software fees.

The platform’s ability to generate consistent, high-quality content across multiple formats means that even personal projects can achieve a professional finish. From personal blogs to experimental art installations, GizAI’s free, no sign up policy makes it accessible to anyone with a passion for creativity. (Inline Source links)

How to Get Started with GizAI

Starting your creative journey with GizAI is remarkably simple. Here’s how you can dive into the world of free AI-powered content creation:

1. Visit the GizAI Website: Go directly to the GizAI website and browse through its array of features and functionalities. The intuitive design allows you to explore various tools without needing to create an account first.

2. Try It for Free: Click on the “Try for free, no login” option to instantly access the AI generators. Whether you’re interested in AI Chat, AI Video, or even interactive story creation, there’s a dedicated tool ready to use.

3. Explore Multiple Formats: Experiment with different response formats—whether it be dynamic text, mind maps, or media-included outputs—to see which one best fits your creative needs.

4. Collaborate and Save: Utilize GizAI’s real-time collaboration features if you’re working with a creative team, and take advantage of integrated cloud storage to securely save your projects for later edits.

5. Expand Your Creativity: Take on new projects like interactive storytelling, digital marketing campaigns, or even educational content. The versatility of GizAI enables you to explore a wide range of creative disciplines without changing platforms.

The process is designed to be as frictionless as possible, ensuring that you spend your time creating rather than managing subscriptions or sign up processes.

The Future of Free AI Content Creation with GizAI

The landscape of AI content creation is evolving rapidly, and GizAI is well-positioned at the forefront of this revolution. As more creatives and professionals demand accessible, high-quality AI tools that do not require mandatory registration or expensive subscriptions, GizAI continues to innovate and expand its features.

Future updates promise even more powerful integrations—such as enhanced collaborative features, seamless integration with third-party applications, and further support for emerging creative formats. The platform’s commitment to privacy and no-data-sharing policies is set to inspire confidence among a broader user base, encouraging even more professionals to test the limits of what AI-powered creativity can achieve. (Inline Source links)

Moreover, as digital transformation continues to dominate every industry from advertising to education, the need for platforms like GizAI that democratize access to advanced AI tools will only grow. GizAI’s blend of advanced technology, user-friendly design, and ethical data management practices positions it as the go-to platform for anyone looking to harness the power of AI without any administrative hurdles.

Real User Reviews and Community Impact

User testimonials are a strong testament to the effectiveness of GizAI. Creative professionals and educators alike have praised the platform for its ease of use and robust functionality. Many have noted that the no sign up, free access policy has revolutionized the way they approach content creation—allowing them to explore diverse ideas, collaborate with peers, and launch projects faster than ever.

Communities ranging from digital marketing groups to independent filmmakers have formed around the GizAI ecosystem, creating an environment rich in shared knowledge and creative inspiration. These communities contribute to continuous improvements and feature requests, making GizAI not only a cutting-edge platform but also a user-driven tool that evolves based on real-world needs and feedback. (Inline Source links)

Final Thoughts: Embrace the Future of Free AI Creativity

GizAI is more than just an AI-powered content creation tool—it is a revolutionary platform transforming the creative landscape by removing barriers and making premium technology accessible to all. With its robust suite of features that span across text, image, video, audio, and interactive storytelling, GizAI empowers everyone from digital marketers and educators to artists and developers.

The no sign up, free access model is a breath of fresh air in an industry typically burdened with subscription fees and cumbersome registration processes. Instead of focusing on monetization through sign ups, GizAI places the creativity and innovation of its users at the heart of its mission—ensuring that AI truly remains an accessible, human right.

By leveraging GizAI’s comprehensive suite of tools, you can embrace your creative potential fully and effortlessly. Whether you need to craft engaging narratives, produce visually compelling graphics, or collaborate on dynamic multimedia projects, GizAI is designed to meet your every need without slowing you down with administrative overhead.

As we look to the future, platforms like GizAI are setting the benchmark for what advanced AI content creation should be—intuitive, powerful, accessible, and secure. Step into the world of free AI creativity and see how GizAI can transform your creative process today.

Experience the freedom to innovate, share, and create without limits. Embrace GizAI’s all-in-one ecosystem for free, no sign up AI tools, and join a growing community of creative professionals who are redefining what’s possible in digital content creation. (Inline Source links)

By choosing GizAI, you’re not only opting for a tool—you’re committing to a movement where access to technology is a right, and creativity is limitless. Enjoy the power of cutting-edge AI at your fingertips, and let GizAI be your partner in crafting the future of content creation.

In recent years, the promise of Artificial General Intelligence (AGI)––AI capable of performing any intellectual task that a human being can––has captured the public imagination and ignited fierce debates across technological, industrial, and political circles. Major tech CEOs and renowned AI experts have offered divergent timelines and predictions regarding when AGI might become a reality. This article examines the detailed landscape of these predictions while exploring the technological challenges, societal implications, and economic consequences of AGI development. We will also review insights from key players such as DeepMind’s Demis Hassabis, Anthropic CEO Dario Amodei, OpenAI’s Sam Altman, and others to provide a comprehensive analysis of the trajectory toward human-level and superintelligent AI.

AGI: Defining the Challenge

AGI is typically defined as an AI system that exhibits the full range of human cognitive abilities. Unlike narrow AI—which is designed to excel at a specific task such as image recognition or language translation—AGI must generalize its learning across multiple domains, adapt to unforeseen scenarios, and ultimately match or even surpass human capabilities. As Google DeepMind CEO Demis Hassabis famously explained, AGI would be “a system that’s able to exhibit all the complicated capabilities that humans can” (“Google DeepMind CEO Predicts A Decade-Long Wait For AI To Match Or Surpass Human Intelligence Across All Domains”).

Despite significant progress in language models and algorithmic planning, current systems remain “very passive,” lacking the breadth and depth required to navigate the complexity of the real world. Transforming these narrow successes into a robust, general intelligence that understands context, reason, and abstract concepts stands as one of the most formidable tasks in the field.

Diverging Predictions Among Big Tech Leaders

Tech leaders across the globe have provided a wide range of forecasts regarding the timeline for achieving AGI. On one end of the spectrum, some experts are optimistic about early breakthroughs, while on the other, more cautious voices argue for a longer developmental horizon.

Demis Hassabis – A Decade Away

Demis Hassabis of Google DeepMind has been one of the most measured voices in the arena. Speaking at a recent briefing in London, Hassabis predicted that the first forms of AGI might emerge in the next five to ten years (“Human-level AI will be here in 5 to 10 years, DeepMind CEO says”). Although he acknowledged that current AI technologies excel at certain specific tasks, he stressed that significant research remains before these systems can operate with the generalized intelligence of a human being.

A primary focus for DeepMind has been on developing “world models” that help an AI understand its real-world context, combined with advanced planning algorithms to bridge the gap between game-like environments and the real world. Hassabis highlights that much of the challenge involves generalizing the successes from highly controlled environments––such as strategy-based simulations like Starcraft––to the unpredictable dynamics of everyday human situations.

Dario Amodei – AGI Sooner Than Expected

In contrast to Hassabis’ cautious timeline, Dario Amodei of Anthropic is among the more optimistic voices in the industry. Amodei has expressed confidence that AI systems capable of outperforming humans at almost all tasks could emerge in as little as two to three years (“Tech Giants, Stop Trying to Build Godlike AI”). He argues that current progress in generative AI and the rapid scaling of technologies are evidence that we are closer than many believe to solving the generalization problem.

Amodei’s perspective is rooted in the belief that the computational and data-driven advances of recent years have set the stage for a leap forward. With improvements in training techniques and the explosive growth in compute power, Anthropic’s vision is that iterative progress in AI can quickly accelerate into a breakthrough in general intelligence.

Sam Altman – The Countdown Is On

OpenAI CEO Sam Altman has provided his own distinctive timeline. Altman has sometimes described AGI as “a few thousand days away,” hinting that the arrival of the first AI agents with human-level reasoning capabilities might be observable within the next few years (“Sam Altman: ‘We Know How to Build AGI’ Eyes 2025 for OpenAI’s First AI Agents”). Altman’s focus is on the practical deployment of AI systems that, while not reaching full AGI immediately, will serve as stepping stones toward a more general intelligence. In recent interviews, he has stressed that even if AGI is not fully realized in the immediate product roadmap, the existing trends indicate a rapid, continuous evolution in AI capabilities.

Elon Musk and Other Cautionary Voices

Tesla CEO Elon Musk has repeatedly sounded caution regarding the pace of AGI development, warning that the advent of AGI could lead to unforeseen consequences and severe societal disruptions (“No AGI But A ‘Killer App’ – 2025 AI – 1 out of 10 Predictions about AI”). Musk has predicted that the arrival of AGI could be as early as 2026, though in his public statements, he has often emphasized the existential risks it poses. His pronouncements serve as a reminder that while the tech race accelerates, the need for robust safety measures and regulatory oversight grows in parallel.

Adding to the caution are experts like Yann LeCun, Meta’s Chief AI Scientist, who has criticized overly optimistic AGI timelines. In various interviews, LeCun has claimed that the current approaches—predominantly based on large language models—are not likely to deliver AGI without entirely new architectures (“Meta’s head of AI: Yann LeCun does not believe in the future of generative AI”). LeCun’s arguments underline that significant conceptual and architectural innovations are still required for AI to achieve genuine human-like intelligence.

International Perspectives and Government Implications

The debate on AGI is not confined to Silicon Valley. International tech leaders and policymakers are closely monitoring AI’s rapid progression. For example, Robin Li from Baidu has suggested that AGI might be more than ten years away, emphasizing that breakthroughs are likely to emerge from continued advances in both technology and understanding rather than abrupt, unprecedented shifts (“Baidu unveils reasoning AI model to regain ground against DeepSeek”).

Government perspectives are equally varied. Some policymakers believe that accelerating AI development could have profound military and economic implications, potentially leading to a global shift in power dynamics. The Biden administration’s approach, discussed by former special AI adviser Ben Buchanan in a recent podcast, highlights that the U.S. government is preparing for a future in which AI systems fundamentally alter the geopolitical landscape (“The Government Knows A.G.I. is Coming”).

The Technological Hurdles to Achieving AGI

Achieving AGI requires overcoming several formidable challenges that are both technical and conceptual in nature:

1. Generalization Across Domains

While narrow AI systems can successfully master specific tasks, they struggle to generalize learning to entirely new domains. Current models tend to excel within the confines of detailed datasets and controlled environments, but real-world applications require far broader understanding and adaptability. Developing algorithms that can transfer knowledge from one area to another remains a fundamental research challenge.

2. Contextual Understanding and World Models

For AGI to be effective, it must understand and interact with the real world with human-like contextual awareness. Hassabis has emphasized the development of world models that allow AI to interpret its surroundings, draw inferences, and plan accordingly (“Google DeepMind CEO Predicts A Decade-Long Wait For AI To Match Or Surpass Human Intelligence Across All Domains”). Successfully combining these models with robust planning algorithms is seen as key to transitioning from narrow AI to AGI.

3. Multi-Agent Systems and Coordination

One promising research avenue is the development of multi-agent AI systems. These approaches involve training multiple AI entities to communicate, collaborate, and sometimes compete in a shared environment. As illustrated by DeepMind’s work on Starcraft, enabling effective interaction between agents is crucial for developing systems that can perform complex, coordinated tasks. This paradigm could serve as a scaled-down model for the broader communication and cooperation needed in AGI.

4. Computational Power and Algorithmic Efficiency

Advances in hardware, such as quantum computing and increasingly powerful GPUs, have been instrumental in speeding up AI research. Nevertheless, scaling these resources efficiently remains a critical issue. The exponential growth predicted by Moore’s Law, though challenged in recent years, still points to a future where computational resources might eventually catch up with our ambitions for AGI. However, the cost and practical limits of such scaling are subjects of ongoing debate among researchers.

5. Ethical and Governance Challenges

Beyond technical hurdles, the development of AGI raises significant ethical questions. The risks associated with systems that can outthink humans are enormous––from job displacement to potential misuse in military contexts. Tech leaders like Elon Musk have warned about the possible societal upheavals that could accompany the arrival of AGI (“Google DeepMind CEO says that humans have just over 5 years before AI will outsmart them”). As such, incorporating measures for safety, accountability, and responsible deployment is as important as the technical work itself.

Societal and Economic Implications of AGI

The eventual emergence of AGI could redefine nearly every aspect of modern civilization. Some of the most pressing areas of impact include:

1. Labor Markets and Job Displacement

AGI systems, with their ability to perform a broad range of cognitive tasks, will likely disrupt traditional labor markets. While AI agents could increase productivity and efficiency by automating routine and even complex decision-making tasks, they also carry the risk of significant job displacement. Policymakers and business leaders will need to design strategies that balance the benefits of increased efficiency with the societal costs of unemployment and economic inequality.

2. Global Economic Competition

The race to develop AGI is not merely a scientific challenge but a crucial element of global economic competition. Nations that succeed in building AGI are likely to dominate key industries, from finance to healthcare, and could secure significant geopolitical advantages. Many experts believe that the country that first harnesses the power of AGI will shift the balance of military, economic, and political power on the world stage (“The Government Knows A.G.I. is Coming”).

3. Ethical Governance and Societal Trust

One of the most contested areas in the AGI debate is how to manage the profound ethical implications of a technology that may one day rival or surpass human intelligence. Ensuring that AGI is developed in a manner that respects human rights, privacy, and dignity is a challenge that will require unprecedented levels of collaboration across regulatory bodies, academic institutions, and tech companies. A failure to establish robust governance frameworks could result in social unrest and a loss of public trust.

4. Innovation and Productivity Gains

On the optimistic side, AGI could drive incredible levels of innovation and productivity gains across diverse sectors. With AI systems that understand and adapt to complex problems, industries ranging from biomedical research to environmental management could see breakthroughs that have long been out of reach. For instance, more intelligent systems could dramatically reduce errors in medical diagnosis or optimize supply chains with far greater efficiency than current technology allows.

5. Cultural and Philosophical Shifts

The arrival of AGI would not only transform economies and labor markets but also provoke deep cultural and philosophical debates about what it means to be human. Questions about consciousness, self-determination, and the nature of intelligence will take center stage. As society grapples with these issues, there will be a need for public engagement and education to ensure that the transition to an AI-augmented world is both democratic and ethical.

Reinforcing the Discussion with Additional Predictions

In addition to the predictions of the aforementioned CEOs and experts, other influential voices in the field provide further context to the debate around AGI timelines:

• Robin Li, CEO of Baidu:
  Li has sparked discussion by suggesting that AGI may be more than a decade away. His perspective is grounded in the belief that while current AI research is yielding impressive results in narrow domains, the leap to true generalization requires breakthroughs that have yet to be achieved (“Baidu unveils reasoning AI model to regain ground against DeepSeek”).

• Yann LeCun of Meta:
  LeCun’s skepticism regarding current large language models’ potential to reach AGI underscores the need for new methodologies. He has urged the community to move away from over-reliance on scaling up existing models and instead explore innovative architectures that mimic human cognitive processes more holistically (“Meta’s head of AI: Yann LeCun does not believe in the future of generative AI”).

• Masayoshi Son:
  The Japanese billionaire investor and CEO of SoftBank has also weighed in, predicting that AGI might emerge within two or three years. Son’s predictions emphasize the dramatic shifts in technology consumption and innovation cycles, although these optimistic timelines are met with both enthusiasm and skepticism across the industry.

• Government and Policy Voices:
  Figures like Ben Buchanan, a former AI adviser in the Biden administration, have warned that the government needs to prepare for the societal impact of AGI. Buchanan’s insights resonate with many policymakers who argue that while the exact timeline may be uncertain, the profound implications of AGI for national security, economic stability, and societal norms are clear (“The Government Knows A.G.I. is Coming”).

Balancing Progress and Caution: A Roadmap for the Future

Given the divergent opinions on when—and whether—we will reach the AGI milestone, it is important to chart a balanced path forward. Here are some key recommendations for industry leaders, governments, and researchers:

Research and Collaboration

• Interdisciplinary Research:
  AGI development is not solely a computer science challenge. It requires the collaboration of experts in neuroscience, cognitive science, ethics, and law to build systems that are not only intelligent but also aligned with human values.

• Open Collaboration:
  While competition drives innovation, open exchanges of ideas and cross-institutional collaboration can accelerate progress and help mitigate risks. Many AI research groups now advocate for shared datasets, benchmark challenges, and joint projects that focus on responsible development.

Policy and Regulation

• Develop Robust Frameworks:
  National and international regulatory bodies must establish guidelines to ensure that AGI development is safe, ethical, and beneficial. These frameworks should focus on transparency, accountability, and the ethical deployment of AI systems.

• Engage Diverse Stakeholders:
  Policymakers should include voices from academia, industry, civil society, and underrepresented communities in policy discussions to ensure that the diverse impacts of AGI are considered. This collaborative approach can help build a more secure, inclusive, and balanced future.

Economic and Social Adaptation

• Workforce Transformation:
  As AI systems become more capable, organizations and governments must invest in workforce retraining and education programs to prepare workers for the transition. Strategies for elevating human skills that complement AI and foster collaboration between humans and machines are crucial.

• Safety Nets and Ethical Investments:
  Economic policies that provide safety nets for displaced workers and ensure that the benefits of AI innovations are broadly distributed should be prioritized. As AGI development ramps up, not only efficiency gains matter but also social equity and ethical investment practices.

Fostering Innovation While Managing Risks

• Incremental Progress:
  Recognizing that AGI will likely emerge as the result of many incremental improvements rather than one sudden breakthrough can help set realistic expectations. This incremental approach allows society to adapt gradually, providing time to implement safety protocols and public policy measures.

• Emphasis on Practical AI Applications:
  While the pursuit of AGI is exciting, immediate gains from narrow AI applications in industries such as fintech, healthcare, logistics, and customer service remain critical for driving economic value. Focusing on concrete, measurable advancements can build public trust and drive sustainable progress.

Conclusion

The race toward Artificial General Intelligence represents one of the most profound scientific and technological challenges of our time. From the measured outlook of Demis Hassabis at DeepMind to the optimistic predictions of Dario Amodei and the cautious warnings of Elon Musk and Yann LeCun, the debate over AGI’s timeline is as complex as it is consequential. While breakthrough predictions vary—from a few years to over a decade—the consensus remains that the arrival of AGI could fundamentally alter the global economic landscape, redefine labor markets, and pose unprecedented ethical challenges.

As governments, corporations, and research institutions scramble to prepare for this transformative technology, collaborative efforts across disciplines and sectors will be essential. Only through responsible innovation, transparent regulation, and inclusive dialogue can we hope to harness AGI’s potential benefits while mitigating its risks.

By balancing ambitious technological progress with prudent ethical considerations, society can navigate the tumultuous journey toward AGI and unlock a future where artificial intelligence works in harmony with human values.

FAQ

Q1: What is Artificial General Intelligence (AGI)?
A1: AGI refers to an AI system that can perform any intellectual task that a human can. Unlike narrow AI, which is tailored to specific tasks, AGI represents a form of intelligence that generalizes across various domains and possesses the full scope of human cognitive capabilities (“Google DeepMind CEO Predicts A Decade-Long Wait For AI To Match Or Surpass Human Intelligence Across All Domains”).

Q2: What are the differing predictions about when AGI will arrive?
A2: Predictions vary widely among industry leaders. Demis Hassabis of DeepMind predicts that AGI may emerge in five to ten years, whereas Dario Amodei from Anthropic is more optimistic, suggesting it might appear in as little as two to three years. Meanwhile, figures such as Elon Musk and Sam Altman forecast early breakthroughs, while cautionary voices like Yann LeCun argue that significant architectural innovations are required before AGI is feasible (“Tech Giants, Stop Trying to Build Godlike AI”; “Meta’s head of AI: Yann LeCun does not believe in the future of generative AI”).

Q3: What are the biggest technical challenges in developing AGI?
A3: Key challenges include enabling AI systems to generalize across various domains, developing robust world models for contextual understanding, improving multi-agent communication and coordination, scaling computational resources effectively, and addressing the ethical and governance issues related to deploying such powerful technologies (“Google DeepMind CEO Predicts A Decade-Long Wait For AI To Match Or Surpass Human Intelligence Across All Domains”).

Q4: How will AGI affect the global economy and society?
A4: AGI could drive tremendous economic growth by unleashing new levels of innovation and productivity across industries. However, it also poses challenges such as job displacement, increased economic inequality, heightened geopolitical competition, and ethical dilemmas regarding the deployment of such advanced technologies. Balancing these benefits and risks requires careful planning, regulations, and societal adaptation (“The Government Knows A.G.I. is Coming”).

Q5: What steps can be taken to prepare for AGI?
A5: Preparing for AGI involves fostering interdisciplinary research and international collaboration, developing regulatory frameworks that ensure ethical and safe research and deployment, investing in workforce retraining programs, and focusing on practical AI applications that deliver immediate economic benefits while building public trust in the technology.

By synthesizing insights from major tech innovators and integrating perspectives across technical, economic, and ethical domains, this article provides a comprehensive roadmap for understanding and preparing for the future of artificial general intelligence. As the race heats up, the decisions made in the coming years will shape our collective future in ways that are both profound and far-reaching.

Artificial intelligence is rapidly transforming how we work, create content, and interact with technology. With so many free AI tools now available, there’s never been a better time to explore and incorporate these cutting-edge solutions into your daily workflow. In this comprehensive guide, we explore a wide range of free AI tools—including productivity assistants, content generators, image editors, and research solutions. We’ll also highlight industry-leading platforms like GizAI, Google AI Studio, and even revisit ChatGPT’s free usage model, ensuring you have all the essential links and insights to get started.

Why Free AI Tools Are a Game-Changer

Many individuals and businesses are attracted to AI solutions not only because they offer innovative ways to solve problems, but also because they often come with free plans or trials. This allows users to experiment with various functionalities, from generating creative copy to enhancing productivity, without any upfront cost. The accessibility of these free tools democratizes technology, enabling startups, freelancers, educators, and even hobbyists to leverage AI for content creation, research, and daily productivity.

ChatGPT: A Free Tier That Delivers

One of the most talked-about free AI tools is ChatGPT, developed by OpenAI. With a free tier that allows users to explore large language model capabilities, ChatGPT has become a household name. The free plan offers access to GPT-4o–the optimized version of ChatGPT–with a limited number of queries per five-hour window. Free users benefit from features such as interactive conversation support, creative brainstorming, coding assistance, translation, and even file uploads for enhanced context during discussions.

For those looking to experiment with conversational AI without a subscription, ChatGPT’s free tier provides an accessible path to experience state-of-the-art natural language understanding and generation. Upgrade options such as ChatGPT Plus offer higher rate limits and faster responses, but the free tier remains a robust option for many everyday tasks.

GizAI: A Versatile Platform for Multimedia and Collaboration

When it comes to integrating multiple productivity and creative tools into one platform, GizAI stands out as a truly innovative solution. It is an all-in-one productivity environment that combines cloud storage, AI-driven chats, multimedia content creation, and note-taking—all under one subscription. GizAI is designed with both casual users and professionals in mind, offering a free plan that supports essential functions like:

• AI Content Generation: Generate text, images, audio, and even video from simple prompts.

• Collaborative Notes: Create and share notes in real-time, complete with AI-powered editing and enhancements.

• Multimedia Tools: Use AI to generate custom images and videos on the fly, making it perfect for marketers and content creators.

• Cloud Storage: Enjoy 10GB of free cloud storage that integrates seamlessly with the entire platform.

GizAI’s free tier allows users to delve into various AI-powered features without any commitment, making it an attractive option for anyone looking to boost productivity and creativity without spending extra dollars.

Google AI Studio: Empowering Experimentation and Development

For developers and tech enthusiasts, Google AI Studio offers an excellent playground to experiment with generative AI models. This platform allows users to quickly test and refine prompts, with its seamless integration of Google’s Gemini API. With Google AI Studio, you can:

• Experiment with Structured and Chat Prompts: Create custom interactive experiences by providing precise instructions that help the AI generate consistent and high-quality outputs.

• Get Code for Your AI Project: Once you’ve perfected your prompt, you can click “Get code” to export the generated code in your preferred programming language.

• Tune Your Model: Advanced users can modify system instructions and add examples to fine-tune the AI’s behavior to match specific requirements.

Google AI Studio’s user-friendly interface and powerful backend make it a cornerstone for anyone serious about prototyping AI solutions with minimal investment.

Top Free AI Tools for Content Creation and Writing

Producing high-quality content is a challenge, especially under tight deadlines. Fortunately, free AI writing tools are here to help. Here are a few top picks that can help you combat writer’s block and generate engaging content quickly:

Copy.ai

Copy.ai offers an impressive array of free AI-powered writing generators that help create everything from marketing copy to creative blog posts. With an easy-to-use interface, Copy.ai enables users to simply share their ideas, press a button, and watch as the AI crafts compelling content. Its free plan provides a taste of its capabilities, perfect for brainstorming and initial drafts.

Rytr and Sudowrite

For those looking to explore creative writing further, tools like Rytr and Sudowrite offer free trials and robust free tiers that help overcome writer’s block and refine your content. These tools integrate well with both professional and casual writing needs, allowing users to experiment with tone, style, and structure.

Grammarly and Wordtune

Editing and improving the quality of your writing is just as important as generating original content. Grammarly and Wordtune both offer free versions that provide grammar checking, style editing, and tone adjustments, ensuring your final output is polished and professional. These tools are invaluable for non-native speakers and anyone looking to elevate their writing skills.

Free AI Tools for Multimedia Content

In the realm of digital marketing and content creation, visuals play a critical role. Fortunately, there are numerous free AI tools available for generating and editing images, videos, and audio.

DALL·E 3 and Midjourney

For digital artists and marketers looking for innovative image generation solutions, tools like DALL·E 3 offer cutting-edge features to transform text prompts into detailed images. DALL·E 3’s free trial lets you harness powerful image generation capabilities without any upfront cost. Alternatively, Midjourney remains popular among creative professionals for its unique artistic style and iterative improvement process.

Runway and Synthesia

Video generation and editing no longer require high-end equipment or extensive technical know-how. Platforms like Runway and Synthesia offer free trials that empower users to create professional-quality videos with AI assistance. Whether you’re editing marketing content or creating a dynamic presentation, these tools make video production accessible and efficient.

Audio Editing with ElevenLabs and Mustango

AI-driven audio tools are also gaining traction. ElevenLabs and Mustango provide free tiers that allow users to generate clear, high-quality audio content. These platforms are particularly useful for creating podcasts, voiceovers, and even converting text articles into engaging audio formats. In many cases, free users can generate a limited number of audio outputs each month—a great way to test the waters without committing financially.

Image Resizing and Editing: Free AI Tools at Your Fingertips

In today’s digital landscape, images must be optimized for various platforms, from websites to social media. Several free AI-powered image resizing tools can help streamline this process while preserving quality.

Img2Go and Upscale.media

Tools like Img2Go and Upscale.media make it easy to resize images without sacrificing clarity. Img2Go supports multiple file formats including BMP, GIF, JPG, and PNG, while Upscale.media can remove artifacts and enhance image resolution up to 4x its original quality—all for free. These tools are especially popular among web designers and social media influencers who need to maintain high visual standards.

Resize and Icons8 Smart Upscaler

For quick image edits, Resize offers a free online platform that supports basic functions such as cropping, compressing, and watermark removal. Additionally, Icons8 Smart Upscaler uses advanced AI to upscale low-resolution images, ensuring that even small visuals look crisp on high-resolution displays.

Bigjpg and MindOnMap

Other noteworthy free tools include Bigjpg, which leverages AI to enhance image pixel quality, and MindOnMap, which supports high-percentage upscaling and batch processing. These tools are invaluable for photographers and digital artists who require precision editing without the premium price tag.

Clipdrop and Aiseesoft

For more complex image editing tasks, Clipdrop and Aiseesoft offer free elements that include background removal, noise reduction, and even intelligent restoration of blurred images. These tools combine simplicity with powerful AI algorithms, making high-caliber image editing accessible to everyone.

Free AI Tools for Research and Data Analysis

Research is an integral part of any successful project, and AI has developed tools that can greatly simplify this process. Advanced AI models are now capable of combing through vast amounts of data rapidly, presenting it in an easy-to-digest format.

Deep Research by ChatGPT and Google Gemini

ChatGPT Deep Research is one such tool that enables users to get detailed reports on complex topics. This isn’t just about simple fact-finding—it can generate long-form analysis complete with citations and data breakdowns.

Similarly, Google’s Gemini Deep Research offers free research capabilities powered by advanced AI algorithms. Whether you’re looking to understand market trends, analyze academic papers, or simply gather insights for a blog post, these tools crunch the numbers and deliver insights that would otherwise take hours to compile manually.

Perplexity.ai and You.com

Other notable free research-oriented AI tools include Perplexity.ai, an AI search engine that provides detailed, context-aware answers, and You.com, which offers a suite of search and research tools specifically designed to enhance productivity. These platforms offer free access to powerful AI algorithms that can simplify academic research, competitive analysis, and decision-making processes.

Free AI Tools for Project Management and Collaboration

Managing projects and collaborating with teams can be challenging without the right tools. Fortunately, many free AI-powered project management platforms now integrate seamlessly into your daily workflow.

Asana and ClickUp

Popular project management tools like Asana and ClickUp offer free tiers that, when supplemented with AI-driven analytics and task automation, significantly boost productivity. These tools help you keep projects on track by providing intelligent suggestions, streamlining recurring tasks, and integrating seamlessly with other platforms such as Gmail and Slack.

Collaborative Note-Taking Platforms

Furthermore, tools like those available through GizAI bring AI into note-taking and collaboration. With real-time collaborative notes, you can work with your team on shared documents, benefit from built-in AI editing features, and automatically organize your ideas. These functionalities are especially useful for teams that require a dynamic workspace that adapts to the ever-changing demands of modern projects.

Free AI Tools for Scheduling and Customer Service

Effective scheduling and robust customer service remain two critical aspects of a successful business. AI-powered scheduling and customer support tools are now available for free to help manage these tasks effortlessly.

Reclaim and Clockwise

For scheduling and time management, tools like Reclaim and Clockwise help optimize your calendar based on your priorities. Their free versions are designed to automatically schedule meetings, adjust available time slots, and ensure that important tasks are given the attention they deserve without manual intervention.

Tidio and Hiver

On the customer service front, free AI-powered chatbots such as Tidio enable businesses to manage customer interactions efficiently. Integration with platforms like Hiver further streamlines email support, enabling companies to respond to queries faster and provide a better overall customer experience. These tools are crucial for startups and small businesses that need to deliver high-quality support without incurring extra costs.

Free AI Tools for Social Media Management and Marketing

As social media becomes an ever more integral part of digital marketing, free AI tools are stepping in to help manage and optimize your online presence.

Vista Social and FeedHive

Vista Social and FeedHive are excellent examples. These platforms provide free tiers that allow you to schedule posts, analyze engagement metrics, and automatically curate content. By using these tools, marketers can save time while ensuring consistent and targeted social media outreach.

Free Marketing AI Tools

For more tailored marketing applications, platforms such as AdCreative and email subject line generators provide free or trial features to help craft compelling ad copy and optimize email campaigns. These tools use sophisticated AI algorithms to suggest improvements, ensuring that your marketing content resonates with your target audience.

The Future of Free AI Tools

The growing list of free AI tools is a testament to how far technology has come. With innovative platforms like GizAI, Google AI Studio, and ChatGPT continuing to push the envelope in capabilities and ease of use, we are witnessing a democratization of powerful AI technologies. Whether you’re a professional content creator, a small business owner, a researcher, or simply a tech enthusiast, the free tiers offered by these services are designed to help you harness the power of AI without a significant financial commitment.

The future holds even more promise as companies work to refine their free offerings. With incremental improvements in model capabilities, increased integration with everyday devices, and a continuing push towards accessible innovation, users can expect free AI tools to become even more integral to daily operations. These advancements foster a competitive ecosystem where users have the freedom to experiment, innovate, and derive value from technology regardless of budget constraints.

Wrapping Up

In summary, the landscape of free AI tools in 2025 is both exciting and expansive. From ChatGPT’s free conversational AI and robust research capabilities to the multifunctional platform of GizAI, and the experimental power of Google AI Studio, no matter your needs, there’s a free or freemium tool available to enhance your productivity, creativity, and overall digital experience. Other notable names—including Copy.ai, Grammarly, Asana, Reclaim, and Tidio—round out a comprehensive toolkit that ensures everyone can stay ahead in an increasingly AI-driven world.

By taking advantage of these free resources, you not only unlock opportunities for innovation but also future-proof your operations without the burden of subscription fees. As these platforms continue to evolve, their integration into everyday workflows promises to streamline processes, foster creativity, and ultimately drive success for individuals and businesses alike.

Whether you’re crafting content, analyzing research data, editing videos, or managing your social media presence, these free AI tools have the potential to radically transform your workflow and give you that competitive edge. Now is the time to explore these offerings, experiment with different solutions, and discover how AI can make your life easier, more productive, and more connected than ever before.

With the rapid pace of technological advancement, the opportunities provided by free AI tools are only going to expand. Embrace this new era of accessible innovation and take full advantage of the myriad of tools at your fingertips. Start exploring, experimenting, and integrating these free resources into your projects today, and watch as AI transforms the way you work, create, and collaborate for the better.

Disclosure: This article was written by GizAI’s AI Writer as a prompt and has not been edited by humans.

Ripple’s native cryptocurrency, XRP, has experienced a stunning surge in value following major regulatory news and market developments. In a decision that has sent shockwaves through the cryptocurrency industry, the U.S. Securities and Exchange Commission (SEC) recently dropped its appeal against Ripple Labs in a four-year legal battle. This article provides an in-depth analysis of the events leading to the surge, the impact on XRP and the broader crypto market, and what this means for the future of digital assets under evolving regulatory frameworks.

The End of a Four-Year Legal Battle

Ripple Labs, founded in 2012, created XRP as the native asset of the XRP Ledger to facilitate cross-border transactions. However, in December 2020, the SEC accused Ripple of conducting an unregistered securities offering by selling XRP worth approximately $1.3 billion. The lawsuit cast a long shadow over the crypto market, creating a climate of regulatory uncertainty and triggering a dramatic loss in market value for XRP holders—an estimated $15 billion wiped out from XRP’s capitalization over the years.

After years of legal wrangling, U.S. District Judge Analisa Torres delivered a landmark decision in 2023 that partially cleared Ripple by ruling that XRP was not a security when sold on public exchanges. The ruling, however, still left institutional sales in a legal gray zone. The SEC’s intent to appeal the decision maintained an ongoing atmosphere of uncertainty. Now, the SEC’s decision to drop its appeal marks a significant turning point for Ripple Labs and the cryptocurrency industry at large.

Ripple CEO Brad Garlinghouse declared the legal battle over on social media, stating,

“I’m finally able to announce that this case has ended. It’s over. This is a resounding victory for Ripple, for crypto, every way you look at it.”
This statement brought long-awaited relief to investors and market participants who had suffered through volatility precipitated by the lawsuit, and it signaled a new chapter of regulatory clarity.

XRP Price Surge: What Happened?

Following the SEC’s announcement, XRP’s market price soared by approximately 14%, reaching levels around $2.55 to $2.59. The surge in XRP’s price is a direct result of renewed investor confidence after years of uncertainty stemming from regulatory disputes. As the SEC stepped back from its aggressive stance, the market interpreted the decision as recognition of Ripple’s legal arguments and a broader move toward easing the regulatory landscape for cryptocurrency companies.

Key Factors Behind the Price Surge

1. Regulatory Clarity:
   The SEC dropping its appeal has provided long-awaited clarity regarding the legal status of XRP. With the regulatory burden lifting, investors now see fewer risks associated with holding XRP, prompting increased buying interest.

2. Favorable Rulings in Ripple’s Favor:
   The 2023 court decision, which determined that XRP was not a security in secondary market transactions, has now been reinforced by the SEC’s decision to withdraw its appeal. The legal precedent now established is expected to influence future regulatory frameworks for digital assets in the United States.

3. Market Sentiment and Investor Confidence:
   The withdrawal of the SEC’s appeal is seen as a victory for the entire cryptocurrency industry. Ripple’s decisive victory has ignited bullish sentiment among investors who now hope that other crypto regulations may also become more favorable toward digital assets. This sentiment has led to not only a spike in XRP’s price but also an overall boost in market sentiment across the crypto space.

4. Ripple’s Strategic Partnerships and Innovation:
   Ripple’s longstanding efforts to integrate XRP into global financial systems—especially in cross-border payments—continue unabated. The firm has maintained partnerships with banks and payment providers across the world. With the SEC case now behind them, these partnerships are expected to expand further, driving heightened adoption and increased demand for XRP.

5. Wider Regulatory Easing in the Crypto Industry:
   The SEC’s decision to scale back enforcement actions against major players such as Coinbase, Uniswap Labs, and Kraken indicates a broader shift toward a more accommodating regulatory environment for digital assets. This change not only benefits Ripple and XRP but also suggests that the U.S. is moving toward a more crypto-friendly future, further boosting market confidence.

Ripple’s Path Forward: Turning a Legal Battle into a Catalyst for Growth

With the SEC appeal now off the table, Ripple Labs is poised to leverage its legal victory as a springboard for future growth. CEO Brad Garlinghouse has articulated a visionary agenda, urging industry unity and calling for the United States to become the “crypto capital of the world.” This perspective underlines Ripple’s commitment to using its newfound regulatory clarity to expand its global presence and develop innovative blockchain-based payment solutions.

Institutional Adoption and Market Expansion

Ripple’s victory may provide the impetus for increased institutional adoption of XRP. For years, banks and financial institutions have hesitated to engage with digital assets due to unclear regulatory frameworks. Now, with a clear legal precedent affirming that XRP is not a security for retail sales, these players may feel more secure in exploring XRP’s potential as a bridge currency in cross-border transactions.

This potential shift toward more widespread institutional adoption could have a profound impact on XRP’s liquidity and market depth. Historically, institutional involvement tends to catalyze price stability and long-term growth by bringing more robust capital into the market. By addressing regulatory uncertainties, Ripple can focus on nurturing partnerships that foster innovation in global financial systems.

Technological Innovation and Improved Payment Systems

Ripple’s vision extends beyond mere financial performance. The company has been a pioneer in exploring how blockchain technology can revolutionize cross-border payments. XRP’s underlying technology ensures transactions are fast, cost-effective, and scalable, making it an attractive option for global remittance and interbank transactions. With regulatory issues resolved, Ripple is well-positioned to enhance its technological offerings and possibly develop new protocols that further streamline digital payments.

Developments such as RippleNet, Ripple’s global payments network, exemplify how the company marries technology with real-world applications. As more banks and financial institutions integrate Ripple’s technology into their operating models, the practical utility of XRP could increase exponentially, leading to further upward pressure on its value.

Ripple’s Potential Impact on U.S. Crypto Regulations

The SEC’s decision to drop its appeal in the Ripple case could have far-reaching implications for the entire cryptocurrency industry. Regulatory clarity in this case sets a significant legal precedent, one that may encourage the SEC and other regulatory bodies to adopt more balanced and clear regulatory frameworks for digital assets. This, in turn, could spur an environment in which innovation is rewarded rather than stifled.

Under new leadership and an evolving regulatory philosophy, the U.S. government appears to be pivoting toward an approach that recognizes the unique challenges and opportunities presented by cryptocurrencies. With clearer guidelines, crypto companies may now feel empowered to innovate without the persistent threat of legal jeopardy. Ripple’s success in navigating these legal hurdles may serve as a blueprint for other companies struggling with similar regulatory battles.

Technical Analysis: Signs That XRP Is Ready for a Major Rally

Beyond the legal and regulatory developments, technical indicators in XRP’s recent price movements suggest that the asset may be preparing for a significant rally. In the days leading up to the recent surge, XRP had traded lower, with technical analysts noting oversold conditions and a falling wedge pattern in the Relative Strength Index (RSI). Such patterns are often precursors to a robust price reversal.

Key Chart Indicators

• Relative Strength Index (RSI):
  The RSI for XRP had been declining over several weeks, descending into oversold territory. A bounce in RSI levels is typically interpreted as a sign that the selling pressure has exhausted itself and that the asset is ready for a rebound.

• Fibonacci Retracement Levels:
  Traders have identified short-term support levels around key Fibonacci retracement levels. Once these levels hold, they provide a technical foundation for price appreciation. The recent rally past critical support levels reinforces the likelihood of further upward movement.

• Volume Spikes:
  The surge in XRP’s price has been accompanied by increases in trading volume, suggesting that the bullish sentiment is supported by substantial market activity. High trading volumes are essential for sustaining a rally, as they reflect genuine investor interest rather than short-term speculative moves.

• Moving Averages:
  Short-term moving averages (such as the 50-day and 200-day moving averages) have begun to converge, a technical signal that often indicates the end of a downtrend and the beginning of upward momentum. With these technical factors aligning, analysts have expressed cautious optimism about XRP’s ability to sustain its recent gains.

Market Outlook: Ripple’s Ripple Effect on the Crypto Industry

The SEC’s decision to drop its appeal and the subsequent surge in XRP’s price have not only benefited Ripple but have also had a positive ripple effect on the broader crypto market. As regulatory clarity improves, other digital assets may witness increased investor confidence and renewed institutional interest.

Broad Market Sentiment

Investors across the cryptocurrency spectrum are taking note of the shift in regulatory tone. With the SEC scaling back its aggressive stance on several high-profile enforcement cases, the overall environment appears to be transitioning toward one of cautious optimism. This development has potential implications beyond XRP:

• Increased Liquidity and Market Stability:
  As regulatory uncertainties diminish, capital that had been on the sidelines may return to the market, increasing liquidity and helping stabilize prices across multiple digital assets.

• Enhanced Global Adoption:
  With the U.S. potentially emerging as a leader in crypto-friendly policy, global investors may perceive an added layer of security when investing in U.S.-based digital assets. This could spark an influx of international capital and foster further adoption of cryptocurrencies.

• Future Regulatory Precedents:
  The positive legal resolution experienced by Ripple could serve as a benchmark for future cases involving digital assets. Other crypto companies facing regulatory battles may draw on Ripple’s experience to negotiate better outcomes or to lobby for clearer, more beneficial regulatory standards.

Institutional Implications

The SEC’s retreat from the enforcement landscape, combined with Ripple’s legal victory, has significant implications for institutional investors. Historically, regulatory clarity has been a prerequisite for many institutional investors to enter the market. With longstanding legal battles behind them, crypto-focused institutional funds may now find it more attractive and less risky to deploy capital into digital assets, including XRP.

Institutional involvement typically leads to greater price stability and can fuel long-term growth by providing a steady influx of capital. Furthermore, as wider participation drives liquidity, price manipulation—often a concern in the crypto markets—may become less of an issue, further reinforcing investor confidence.

Challenges and Opportunities Ahead

While the recent surge in XRP’s price is undoubtedly a positive development, Ripple and the crypto industry still face several challenges. Navigating the transition from an era defined by regulatory uncertainty to one characterized by clearer guidelines will require strategic adjustments and ongoing innovation.

Remaining Regulatory Questions

Despite the positive outcome in the Ripple lawsuit, some regulatory questions remain unresolved. For instance, while retail sales of XRP are now clarified as not constituting a security, the classification of institutional sales is still a contentious issue. Ripple may need to consider further legal steps or adjustments in its market strategy to address these concerns comprehensively.

Moreover, as other regulators worldwide take note of the U.S. decision, there may be pressure to harmonize regulatory frameworks internationally. Ripple’s ability to adapt to these evolving global standards will be a crucial determinant of its long-term success.

Technological and Operational Challenges

As Ripple expands its global outreach and deepens its integration with financial institutions, it must continuously upgrade its technological infrastructure. The demands of real-time cross-border payments, high transaction throughput, and enhanced security are ever-increasing. Ripple’s continued investment in blockchain technology and innovation will be critical to maintaining its competitive edge.

In addition, operational risks such as cyber threats and technical glitches—though not new to the industry—remain an inherent challenge. Ripple’s track record in securing its platforms and maintaining robust operational practices will need to be exemplary to instill further confidence among its current and potential users.

Expanding Use Cases Beyond Payments

Another significant opportunity for Ripple lies in expanding the use cases of XRP. While its primary function remains facilitating seamless cross-border transactions, XRP can also act as a bridge asset in emerging areas such as decentralized finance (DeFi) and central bank digital currencies (CBDCs). As governments and financial institutions explore alternative digital payment systems, Ripple’s expertise in blockchain technology positions it well to capture new market segments.

If Ripple can successfully diversify its applications for XRP, it could unlock additional demand drivers that further support its price and market capitalization over the long term.

Expert Opinions and Price Predictions

The recent developments have led to a flurry of analyses and price predictions from renowned market analysts and technical experts. Many have noted that XRP’s current trajectory, buoyed by both legal and technical fundamentals, could set the stage for a sustained rally.

Some technical analysts highlight that important support levels around $2.20 to $2.30 need to hold for further upside, while bullish signals from the RSI and moving averages suggest that XRP might be primed for a long-term upward trend. Predictions range from moderate rallies pushing XRP to mid-$3 levels in the short term, to more ambitious forecasts where XRP could approach $5 or higher in the coming months if institutional adoption accelerates.

Analysts also point to historical trends in the crypto market, noting that when regulatory uncertainty dissipates, capital accumulation follows swiftly. Ripple’s case now stands as a landmark example of how overcoming legal challenges can propel a cryptocurrency from a state of volatility to one of robust growth.

Global Impact: What This Means for the Crypto Industry

Ripple’s legal victory and XRP surge are more than just isolated events; they could herald a paradigm shift for the entire crypto industry. With the SEC’s withdrawal from several high-profile enforcement cases, the broader market is poised to experience a wave of regulatory leniency that may benefit many digital assets.

Shaping Future Registrations and Listings

For crypto exchanges and wallet providers, a clearer regulatory landscape reduces the risk of delistings and freezes on the assets they support. This change is expected to promote a healthier ecosystem where innovation can flourish without the looming threat of sudden regulatory crackdowns. In turn, this environment fosters trust among users and investors alike.

Encouraging Innovation in Financial Services

Banks and financial institutions have long been cautious in integrating blockchain technology due to regulatory ambiguities. Ripple’s clear legal win is likely to accelerate efforts by these institutions to adopt more advanced digital payment systems and explore blockchain-driven solutions. Such innovation not only bolsters Ripple’s market position but also paves the way for further technological breakthroughs across the financial services industry.

Fostering International Regulatory Alignment

Ripple’s experience could serve as a case study for international regulators as they strive to develop harmonized frameworks for digital assets. As countries observe the benefits of clear and balanced regulation, there is an opportunity for a coordinated effort to protect consumers while allowing innovation to thrive. This international alignment could further boost market stability and encourage cross-border collaboration in the emerging digital economy.

Conclusion

The recent surge in XRP’s price, driven by the SEC’s decision to drop its appeal in the legal battle against Ripple, marks a turning point for the cryptocurrency industry. Ripple’s legal victory not only provides critical regulatory clarity but also reinvigorates investor confidence and sets a promising outlook for both XRP and the broader crypto market.

As Ripple embarks on a new phase—characterized by increased institutional adoption, technological innovation, and a more favorable regulatory environment—the entire digital asset ecosystem stands to benefit from the ripple effects. Investors, banks, and technology providers are now better positioned to explore the myriad opportunities that this evolving landscape presents.

While challenges remain, the combination of strong legal precedents and robust technical indicators suggests that XRP is well on its way to establishing itself as a key player in the global digital economy. Market participants will be watching closely as Ripple leverages this momentum to drive further innovation, expand its network of partnerships, and help shape the future of cryptocurrency regulation.

FAQ

Q1: What led to the recent surge in XRP’s price?
A1: The recent surge in XRP’s price is largely attributed to the SEC’s decision to drop its appeal against Ripple in a four-year legal battle. This action removed significant regulatory uncertainty surrounding XRP, boosting investor confidence and leading to a 14% increase in its market value.

Q2: How long did the legal battle between Ripple and the SEC last?
A2: The legal battle spanned over four years, starting in December 2020, during which the SEC accused Ripple of conducting an unregistered securities offering. A ruling in 2023 partially cleared Ripple by stating that XRP was not a security when sold on public exchanges.

Q3: How is the regulatory decision expected to impact the broader crypto market?
A3: The withdrawal of the SEC’s appeal is expected to have a positive ripple effect across the crypto market. It provides regulatory clarity, enhances market sentiment, encourages institutional participation, and may lead to similar easing of regulations for other digital assets.

Q4: What technical signals support XRP’s potential for further growth?
A4: Technical signals include an oversold RSI indicating that selling pressure has eased, supportive Fibonacci retracement levels, increased trading volumes, and converging short-term moving averages (50-day and 200-day). These indicators suggest that XRP may be ready for a sustained rally.

Q5: How might Ripple leverage this legal victory for future growth?
A5: Ripple can use the legal victory to drive wider institutional adoption by reassuring investors that XRP is legally compliant for retail transactions. Furthermore, the company can expand its global network of banking partnerships, further develop its blockchain payment technology, and explore new use cases in DeFi and CBDCs.

Q6: What are the potential challenges Ripple might face moving forward?
A6: Despite the victory, Ripple still faces unresolved regulatory questions regarding the classification of institutional XRP sales and the need for continued technological innovation to address operational challenges. Additionally, global regulatory harmonization and overcoming potential cyber threats remain areas that require ongoing focus.

Reference List at the End

1. Barron’s – “XRP surges after Ripple CEO says SEC drops its case”

2. CNBC – “Ripple’s legal battle and its impact on XRP price”

3. CryptoTimes – “XRP price surges 14% as SEC drops Ripple lawsuit after 4 years”

4. TradingView – “XRP Turnaround Moment? Analyst Says It’s Lift-Off Time”

5. CoinCentral – “Breaking: SEC Drops Appeal in Case Against Ripple, XRP Price Surges”

6. FXEmpire – “XRP Soars 14% as SEC drops appeal – Is a Major Rally Ahead?”

7. Reuters – “Record 2024 temperatures speed up ice loss” (contextual for market reaction insights)

By addressing both the legal and technical narratives, this article showcases how Ripple and XRP are not only overcoming significant past challenges but are also poised to drive future innovations in the cryptocurrency space. The evolving regulatory framework, combined with technological enhancements and renewed investor trust, suggests a promising horizon for XRP and the broader crypto market.

Dicas exclusivas de trading para aumentar seus lucros hoje

O trading é uma atividade que pode proporcionar lucros diários consistentes quando aplicado com estratégia e disciplina. No entanto, muitos traders iniciantes cometem erros que reduzem seu potencial de ganhos. Neste artigo, exploraremos dicas de trading altamente eficazes que podem ajudá-lo a aumentar seus lucros e operar de maneira mais segura no mercado financeiro.

Como otimizar seus investimentos no trading

Para alcançar o sucesso no trading, é essencial entender as nuances do mercado financeiro. Estratégias bem estruturadas, gestão de risco eficaz e o uso correto de análise técnica e fundamentalista são componentes essenciais para um trading lucrativo. Se deseja aumentar seus lucros diários e melhorar seu desempenho, confira abaixo as melhores práticas e segredos do mercado.

1. Domine a gestão de risco no trading

A gestão de risco é um dos pilares fundamentais para qualquer trader. Independentemente da sua experiência, proteger seu capital deve ser uma prioridade. Algumas técnicas eficazes incluem:

• Utilizar o stop loss: Defina pontos de saída para limitar perdas em operações desfavoráveis.

• Gerenciar o tamanho da posição: Ajuste a alocação de capital para cada operação com base na volatilidade e no seu portfólio.

• Usar a regra do 1%: Nunca arrisque mais que 1% do seu capital total em uma única operação.

• Diversificação: Evite colocar todo seu capital em um único ativo.

Gerenciar riscos eficazmente garante que mesmo uma sequência de perdas não comprometa seu capital de trading de maneira irreversível.

⭐⭐⭐⭐⭐Crie Sua Conta Demo na Deriv e Comece Sem Medo!

🚀💡 Lucre Agora com o Programa de Afiliados da Deriv!

2. Aprenda e aplique análise técnica

A análise técnica envolve o estudo de gráficos e padrões do mercado financeiro para prever movimentos futuros de preços. Algumas ferramentas essenciais incluem:

• Médias Móveis: Indicadores que identificam tendências e pontos de reversão.

• Suporte e Resistência: Níveis onde o preço tende a reagir.

• Índice de Força Relativa (RSI): Mede a força do mercado para indicar momentos de sobrecompra e sobrevenda.

• Candlestick Patterns: Formações de velas japonesas que antecipam movimentos.

Ao dominar essas técnicas, você melhora sua capacidade de tomar decisões rápidas e precisas.

3. Utilize a análise fundamentalista ao seu favor

Enquanto a análise técnica se concentra no movimento do preço, a análise fundamentalista avalia métricas financeiras para identificar o valor real de um ativo. Alguns fatores a considerar:

• Resultados financeiros da empresa: Empresas lucrativas geralmente possuem ações mais estáveis.

• Eventos macroeconômicos: Notícias como taxas de juros e inflação impactam diretamente os preços.

• Indicadores de mercado: PIB, taxa de desemprego e balança comercial são dados cruciais.

Combinar análise técnica e fundamentalista permite decisões mais informadas e seguras.

4. Escolha a plataforma de trading ideal

O sucesso no trading também depende da escolha da plataforma correta. Algumas das melhores plataformas incluem:

• MetaTrader 4 e 5: Excelentes para forex e CFDs, com ferramentas avançadas de análise técnica.

• NinjaTrader: Popular entre traders de futuros e ações.

• Interactive Brokers: Indicado para traders que operam com grandes volumes.

Certifique-se de que a plataforma oferece bons recursos de análise e execução rápida para otimizar seu desempenho.

5. Desenvolva um plano de trading sólido

Todo trader bem-sucedido segue um plano bem definido que inclui:

• Objetivos claros: Determine metas diárias, semanais e mensais.

• Estratégias baseadas em dados: Nunca entre em uma operação sem antes analisar o contexto.

• Revisão e otimização: Avalie regularmente seu desempenho e ajuste sua abordagem.

Um plano estruturado reduz a influência emocional e melhora a consistência dos resultados.

⭐⭐⭐⭐⭐Entre na Deriv Hoje e Experimente Sem Compromisso!

🚀💡 Transforme Cliques em Ganhos com a Deriv!

6. Controle seu psicológico e evite erros comuns

O controle emocional é um dos maiores desafios no trading. Um erro emocional pode acabar com meses de lucro em apenas um dia. Técnicas para manter a disciplina incluem:

• Evite overtrading: Operar demais pode levar à exaustão e decisões ruins.

• Aprenda a aceitar perdas: Nem todas as operações serão vencedoras. Aceitar isso faz parte do jogo.

• Defina horários para operar: O excesso de tempo no mercado pode aumentar a exposição a riscos desnecessários.

Manter uma mentalidade disciplinada e estratégica ajudará a maximizar seus ganhos.

7. Teste estratégias antes de operar com dinheiro real

Outro erro comum entre traders iniciantes é testar estratégias diretamente na conta real. Em vez disso:

• Use contas demo: Simule operações sem arriscar dinheiro real.

• Analise sua performance: Veja quais estratégias funcionam melhor para você.

• Otimize seus setups: Ajuste suas estratégias conforme necessário.

Isso permite que você refine suas técnicas antes de colocá-las em prática com capital real.

8. Fique atualizado com as tendências do mercado

Estar sempre informado sobre fatores que influenciam o mercado financeiro é essencial para operações bem-sucedidas. Algumas fontes confiáveis incluem:

• Investopedia: Repleto de artigos e tutoriais educativos.

• TradingView: Ótima para monitoramento de gráficos e análises.

• Notícias econômicas globais: Reuters, Bloomberg e CNBC são fontes valiosas.

Quanto mais informado você estiver, melhor será sua capacidade de antecipar oportunidades lucrativas.

Conclusão

O trading pode ser altamente lucrativo, mas exige conhecimento, disciplina e aplicação de estratégias eficazes. Focar em gestão de risco, análise técnica e fundamentalista, planejamento e controle emocional são aspectos essenciais para garantir operações bem-sucedidas.

Aplique essas dicas e aumente seus lucros hoje mesmo!

⭐⭐⭐⭐⭐Testemunhe os Resultados – Abra Conta Demo Agora!

🚀💡 Ganhe Comissões Atrativas com o Programa da Deriv!

Perguntas Frequentes sobre Trading

1. Qual a melhor estratégia para traders iniciantes?

A melhor estratégia para iniciantes é focar na análise técnica básica e usar uma gestão de risco adequada, começando com operações pequenas para evitar grandes perdas.

2. O que é mais importante: análise técnica ou fundamentalista?

Ambas são fundamentais, mas para operações de curto prazo, a análise técnica é mais útil, enquanto a fundamentalista é melhor para investimentos de longo prazo.

3. Quanto tempo leva para se tornar um trader lucrativo?

Isso varia entre os traders, mas normalmente leva meses ou até anos para desenvolver habilidades consistentes e uma estratégia sólida.

4. Quais são os erros mais comuns de iniciantes no trading?

Os erros mais comuns incluem operar sem um plano, ignorar a gestão de risco, deixar as emoções influenciarem as decisões e não acompanhar tendências do mercado.

5. É possível viver exclusivamente de trading?

Sim, mas exige um alto nível de conhecimento, disciplina e capital suficiente para cobrir despesas e manter a consistência dos lucros.

Agora que você conhece essas dicas exclusivas, comece a aplicar cada uma e veja seus resultados melhorarem! 🚀

Atenção: Este conteúdo não constitui recomendação financeira. Antes de tomar decisões, faça sua própria pesquisa e consulte especialistas para evitar riscos desnecessários.

Referências:

✅Lucro Trader | forex para iniciantes

✅Blog | Lucro Trader

✅Mercados Financeiros: Forex e Binárias

✅Programa de Afiliados Deriv: Ganhar Dinheiro Online 2025

✅Descubra Como Ganhar Dinheiro pela Internet em 2025

✅Deriv Afiliados: Oportunidade de Renda Extra em Dólar

✅Deriv: Corretora Forex de investimentos inteligentes em 2025